검색결과 리스트
2023/11/01에 해당되는 글 16건
- 2023.11.01 검증(檢證)과 검정(檢正)
- 2023.11.01 2. 분석방법을 선택하는 두 가지 기준, 두 번째: 변수의 속성
- 2023.11.01 나. 등분산 검정
- 2023.11.01 가. 정규성 검정
- 2023.11.01 1. 분석방법을 선택하는 두 가지 기준, 첫 번째: 모수통계, 비모수통계
글
검증(檢證)과 검정(檢正)
검증하다와 검정하다는 한글로 쓰면 비슷해보이지만, 그 의미는 분명히 다르다. 게다가 검정하다는 검정(檢定)과 검정(檢正)의 두 가지로 사용된다. 이를 구분하기 위해 영어표현을 살펴보자.

우리가 하는 것은 사회조사를 통해 해당 사실을 test하는 것이다. 따라서 검정(檢正)하다가 정확한 표현이다. 이 test와 관련하여 칼 포퍼(Karl Popper)는 그의 반증이론(The theory of Falsification)을 통해 사회과학에서 100% 확실한 진리를 검증(檢證)하는 것은 불가능에 가까운데, 왜냐하면 언제든 설명되지 않는 부분에서 반증자료가 나타날 가능성이 있기 때문이라 말한다.
그래서 가설은 검정(test)하는 것이지, 검증(verify)할 수는 없다.
'[楞嚴] 생각 나누기 > [平] 사회조사와 데이터분석' 카테고리의 다른 글
| 부등식의 표현 이해 (0) | 2023.11.01 |
|---|---|
| 공(空)과 무(無), 0과 null (0) | 2023.11.01 |
| 2. 분석방법을 선택하는 두 가지 기준, 두 번째: 변수의 속성 (0) | 2023.11.01 |
| 나. 등분산 검정 (0) | 2023.11.01 |
| 가. 정규성 검정 (0) | 2023.11.01 |
설정
트랙백
댓글
글
2. 분석방법을 선택하는 두 가지 기준, 두 번째: 변수의 속성
모수 통계는 평균에 기반한다. 그리고 당연한 얘기겠지만, 분석에 이용되는 자료(변수)는 평균을 구할 수 있는 형태여야만 한다. 즉 변수의 속성이 등간 또는 비율척도여야 한다. 만일 명목 또는 서열척도라면 어떻게 해야할까? 명목척도라면 빈도를, 서열척도라면 중앙값(중위수)을 기준으로 분석하는데, 이를 비모수 통계라 한다.
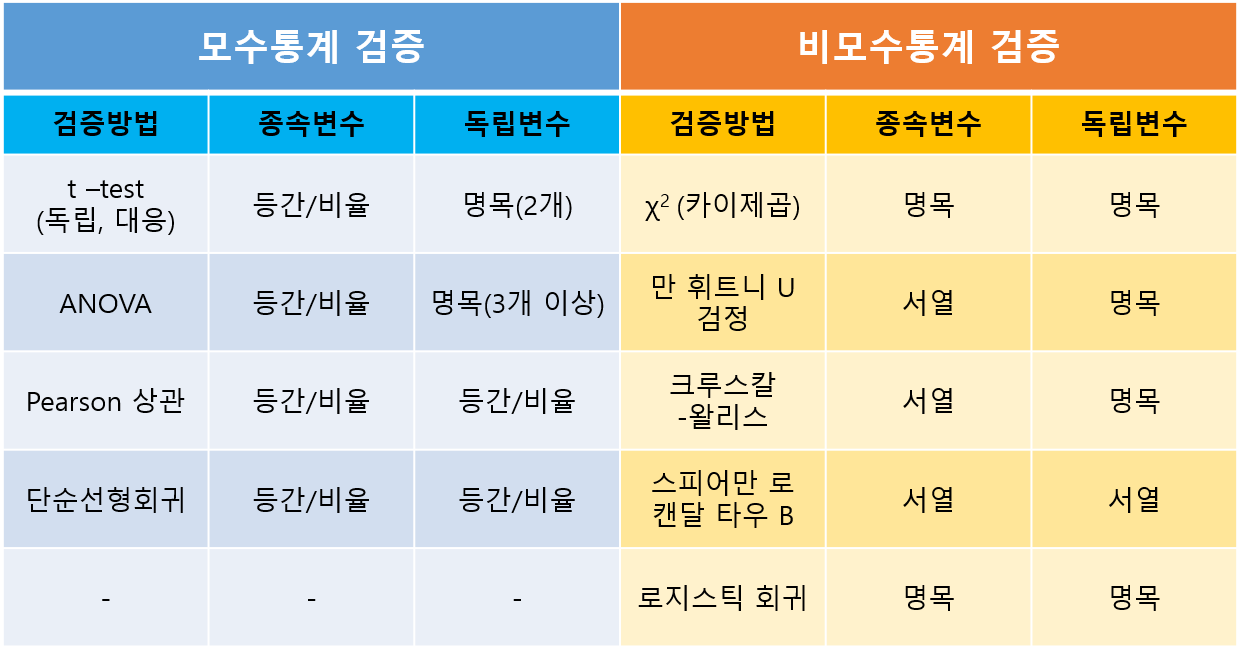
그리고 모수통계와 비모수통계는 다음이 서로 짝을 이룬다.

'[楞嚴] 생각 나누기 > [平] 사회조사와 데이터분석' 카테고리의 다른 글
| 공(空)과 무(無), 0과 null (0) | 2023.11.01 |
|---|---|
| 검증(檢證)과 검정(檢正) (0) | 2023.11.01 |
| 나. 등분산 검정 (0) | 2023.11.01 |
| 가. 정규성 검정 (0) | 2023.11.01 |
| 1. 분석방법을 선택하는 두 가지 기준, 첫 번째: 모수통계, 비모수통계 (0) | 2023.11.01 |
설정
트랙백
댓글
글
나. 등분산 검정
나. 등분산 검정
서로 다른(독립) 두 집단을 비교하고자 한다면, 해당 집단들 간의 분산이 동일한지를 검토해야한다. 이를 등분산 검정이라 한다. 그리고 등분산성은 Levene의 등분산 검정을 통해 확인할 수 있다. 독립표본 t 검정의 경우, 그 결과에 따라 등분산 가정 t 검정을 할지 이분산 가정 t 검정을 할지 결정하게 된다.

등분산 검정 결과 p>.05이면 등분산을 가정한다. SPSS의 경우 독립표본 t 검정을 실시하면 등분산을 가정했을 때와 이분산을 가정했을 때의 결과를 모두 보여준다. 이때 연구자는 Levene's test 결과를 바탕으로 어떤 값을 선택할지 결정해야한다.
'[楞嚴] 생각 나누기 > [平] 사회조사와 데이터분석' 카테고리의 다른 글
| 검증(檢證)과 검정(檢正) (0) | 2023.11.01 |
|---|---|
| 2. 분석방법을 선택하는 두 가지 기준, 두 번째: 변수의 속성 (0) | 2023.11.01 |
| 가. 정규성 검정 (0) | 2023.11.01 |
| 1. 분석방법을 선택하는 두 가지 기준, 첫 번째: 모수통계, 비모수통계 (0) | 2023.11.01 |
| Ⅳ. 어떤 분석방법을 활용할 것인가? (0) | 2023.11.01 |
설정
트랙백
댓글
글
가. 정규성 검정
모수통계의 방법은 모집단의 정규분포를 가정한다. 즉 정규성 여부가 가정되어야만 모수통계를 사용할 수 있다. 이를 위해 Kolmogorov-Smirnov(콜모고로프-스미르노프) 검정과 Shapiro-Wilk(샤피로-윌크) 검정을 활용한다. Kolmogorov-Smirnov test는 n≥30인 경우, Shapiro-Wilk test는 n<30인 경우에 사용하며, 이때 통계량의 p value가 p>.05이면, 정규성을 가정한다.

만일 p<.05이면, 정규성을 가정할 수 없기 때문에 비모수 검정을 사용해야한다.
다만, 이런 검정방법은 매우 엄밀성을 강조하기 때문에 그 활용에는 제약을 받는다. 또다른 방법으로는 왜도와 첨도를 통해 정규성을 가정하는 방법이 있다. 기술통계를 통해 왜도의 절댓값이 2보다 작고 첨도의 절댓값이 7보다 작으면 정규성을 가정하는 것이다.
SPSS를 활용한 정규성 검정은 “데이터 탐색”메뉴에서 찾을 수 있다.
분석 > 기술통계량(E) > 데이터 탐색(E) > (도표) > ☑ 검정과 함께 정규성 도표(O)

만일 표본의 수가 30 이상이면, Komogorov-Smirnov 검정을, 30 미만이면 Shapiro-Wilk 검정의 통계량과 유의확률을 확인하면 된다.
이때, 유의확률 p>.05이면 정규성을 가정한다. 위 예시에서는 표본의 수(n)가 25명이기 때문에 Shapiro-Wilk 검정 결과를 확인해야하며, 통계량 W=.944(p>.05)로 정규성을 가정한다.
한편 왜도와 첨도는 기술통계의 옵션에서 확인할 수 있다.
분석 > 기술통계(D) > (옵션) > 분포에서 ☑ 첨도(K), ☑ 왜도(W) 체크
(덧붙임 2025. 5. 9.) 여러 정규성 검정방법에 대한 비교는 아래와 같다.
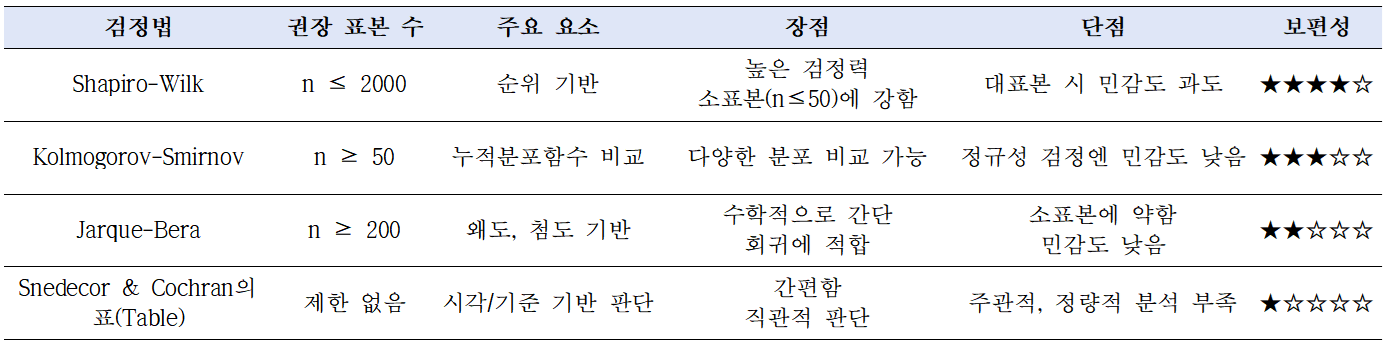
한편 왜도와 첨도를 활용한 탐색적 기준은 아래와 같다.
기준 왜도와 첨도 범위 이내이면 정규성(Hair et al. 2010)을 가정한다고 본다.

'[楞嚴] 생각 나누기 > [平] 사회조사와 데이터분석' 카테고리의 다른 글
| 2. 분석방법을 선택하는 두 가지 기준, 두 번째: 변수의 속성 (0) | 2023.11.01 |
|---|---|
| 나. 등분산 검정 (0) | 2023.11.01 |
| 1. 분석방법을 선택하는 두 가지 기준, 첫 번째: 모수통계, 비모수통계 (0) | 2023.11.01 |
| Ⅳ. 어떤 분석방법을 활용할 것인가? (0) | 2023.11.01 |
| 9. 이제 유의수준, 유의확률, 신뢰수준, 신뢰구간을 비교해보자. (1) | 2023.10.29 |
설정
트랙백
댓글
글
1. 분석방법을 선택하는 두 가지 기준, 첫 번째: 모수통계, 비모수통계
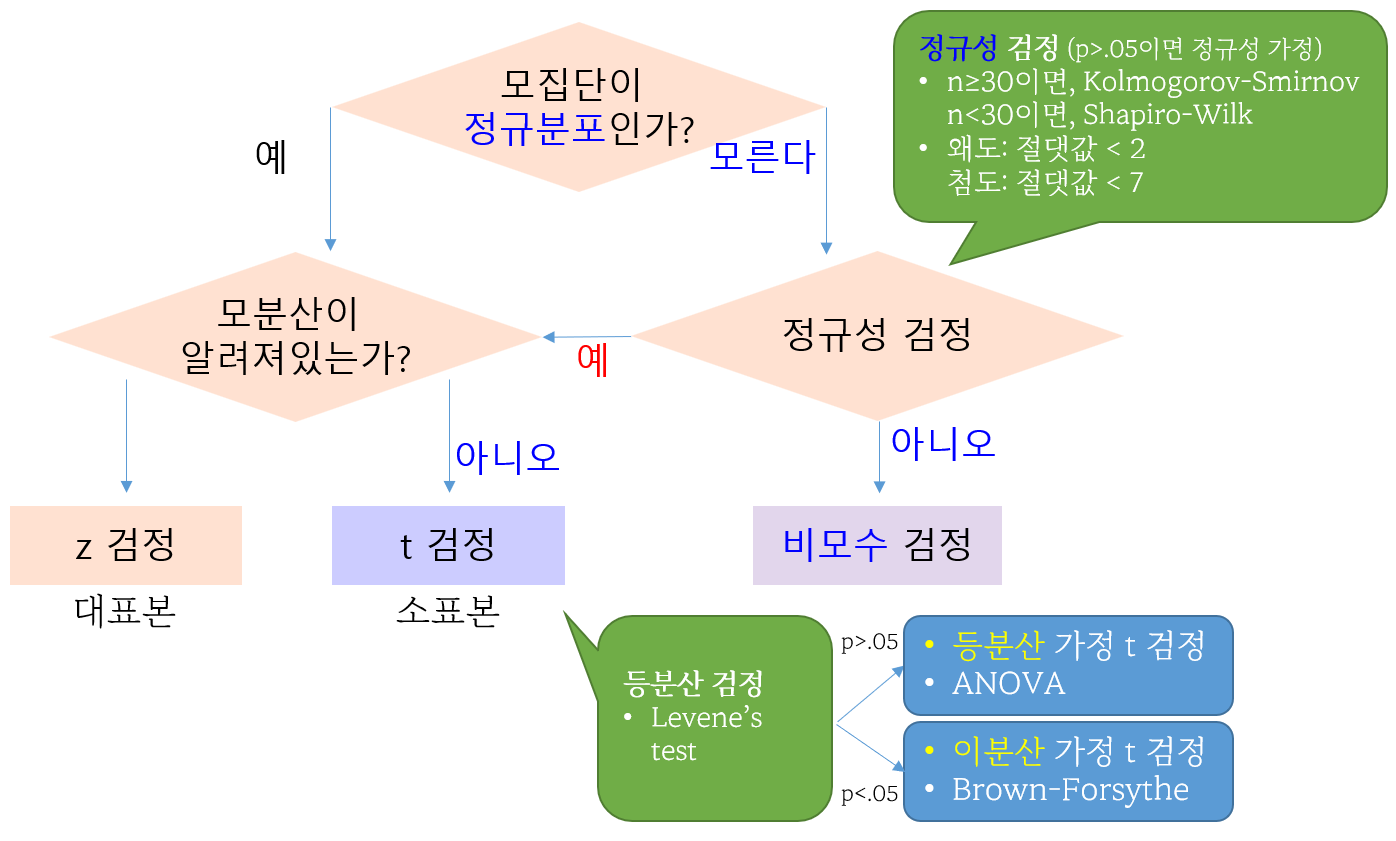
앞서 평균을 구할 수 있으면 모수통계, 없으면 비모수통계라 언급한 바 있다. 보다 엄밀히 말해보자면, 모집단의 분포가 정규분포이고와 모수(평균, 표준편차)를 알고 있다는 가정하에 분석하는 방법을 모수통계라 한다.
'[楞嚴] 생각 나누기 > [平] 사회조사와 데이터분석' 카테고리의 다른 글
| 나. 등분산 검정 (0) | 2023.11.01 |
|---|---|
| 가. 정규성 검정 (0) | 2023.11.01 |
| Ⅳ. 어떤 분석방법을 활용할 것인가? (0) | 2023.11.01 |
| 9. 이제 유의수준, 유의확률, 신뢰수준, 신뢰구간을 비교해보자. (1) | 2023.10.29 |
| 8. 엄정한 실험설계를 위한 연구자의 노력 (0) | 2023.10.29 |

RECENT COMMENT