Social Welfare Thorn News, 福智衍, 복지비틀기

사회복지관에서 왜 환경문제를 다루어야만 하는 것일까요?

환경운동단체의 활동과 차별점은 무엇일까요?

지난 2023년 부산시 주민참여예산 사업으로 必환경&Fee환경 공동체사업을 수행하면서, 1년 간의 성과를 나누는 성과보고서에 실었던 인삿말 전문입니다.

==============================================

사회복지관에서 환경문제를 이야기하려 했을 때 가장 많이 들었던 질문은 “왜 복지관에서?”였습니다. 이미 사회복지실천 현장에서는 환경과 관련한 주제들을 다루고 있었음에도 “왜”라는 꼬리표는 여전히 따라다녔습니다. 그리고 이번 성과보고회는 바로 이 질문에 대한 나름의 대답입니다.

첫째, 환경문제를 사회복지로 어떻게 담아낼 것인가에 대한 이야기입니다.

이에 대한 진지한 고민을 6개의 사회복지관이 각기 다른 이야기로 풀어내었습니다. 미래 세대를 위한 지킴이 활동, 동아리 활동, 업사이클링, 환경을 위한 실천운동 등 참여자도 다르고, 무얼 하는지도 다르지만, 결국 사회복지라는 그림 아래서 풀어내었습니다.

둘째, 혼자가 아닌 함께 나누어야만 하는 이야기입니다.

지금까지 환경을 위해 내가 어떤 활동을 해야 하는가에 방점을 두었다면, 이 이야기는 우리가 ‘함께’ 무엇을 어떻게 할까에 대한 고민입니다. 하여 공동체도 만들고, 네트워크도 만들어 보고, 환경 거점으로의 사회복지관도 고민해 보았습니다.

마지막으로 환경을 통해 같은 공간을 살아가는 사람에 대한 이야기입니다.

환경으로 인한 문제는 결국 우리 모두의 문제이지만 이것 또한 불평등하게 작동한다는 불편한 현실. 미래를 살아갈 우리 아이들, 환경 변화에 취약할 수밖에 없는 이들의 목소리에 대한 대변입니다. 그리고 고맙게도 이에 공감해주는 우리 이웃들의 이야기입니다.

환경!

반드시(必) 다가올 가까운 미래, 사람에 대한 공감(feel)을 기반으로 다함께 노력할 수 있도록, 그 과정에서 마중물이 되고자 여러 사람들과 함께 했습니다.

그 모든 분들께 마음 깊이 고마운 마음을 전합니다.

또한 주민참여예산을 통해 우리들의 이런 고민들과 해법을 실현할 수 있도록 지원해주신 부산시에도 감사를 드립니다.

더불어 걷는 걸음에 함께 해주셔서 다시 한번 감사드립니다.

==============================================

1~3년차 대상 사회복지사 보수교육 강의 교안으로 작성한 내용입니다.

사회복지사로서 생산하게 되는 많은 문서들과 관련하여, 어떠한 규정/원칙에 의거하여 문서를 작성하여야 하는가에 대한 문서작성방법과 한발 더 나아가 그 문서를 어떤 내용으로 채울 것인가에 대한 고민을 담았습니다.

신규프로그램을 기획했을 때, 이용자 모집에 있어 어려움을 겪는 경우가 많다.
우리는 왜 이런 어려움을 겪게 되는가?
단계적으로 하나하나 살펴보자.

우리가 이런 경험을 하게 되는 첫 번째 이유는 충분성의 문제이다.

1. 이용자의 수가 충분하지 않다.
일반적으로 통계자료 등을 통해 표적집단의 수를 대략적으로 파악할 수 있다.
만일 이용자의 수가 충분하지 않다면 해당 프로그램을 기획해서는 안되는 것이었다.
이용자의 수가 적음에도 불구하고 꼭 진행해야하는 프로그램이었다면 casework 적으로 접근해야만 한다.

2. 이용자의 비자발성 때문
사실은 이게 더 본질적인 문제인데, 대부분의 사회복지프로그램은 문제해결에 초점을 두고 있다보니 자발적 참여를 기대하기가 어렵다.
일반적으로 사회복지시설에서 해당 프로그램을 기획했을 때, 홍보를 통해 당사자에게 전달되기까지 많은 손실이 발생한다. 때문에 기본적으로 전달률은 30%가 채 되지 않는다.
여기에 참여의지가 있는 이용자는 대략 10% 수준이다.
결국 프로그램이 필요한 당사자에게 전달되고 참여를 결정하게 되기까지 표적집단의 3~5% 정도가 신청한다고 보면 얼추 맞을 것이다.
100명의 필요 당사자가 있다면 3~5명만이 신청한다는 결론이다.

이때의 해결책은 단순하다.
1의 경우, 5%를 기준으로 참여자의 수가 충분할 것인지에 대해 사전에 검토를 해야한다.
2의 경우를 위해서는 좀더 적극적인 홍보가 필요하다. 일반적으로 참여자 모집정원의 절반 정도는 쉽게 모집이 되는 편이다. 그렇다면 전달률을 높이는 방법을 포함하여 홍보 노력을 지금보다 2배는 더 기울여야 한다는 결론이다. 조직 내부에서 충분한 검토를 하기를 바란다.

두 번째 이유는 윤리성 때문이다.
사회복지 프로그램의 기획은 클라이언트의 욕구보다는 필요성에 근거해서 만들어진다. 
사회복지사로서 판단할 때, 욕구는 있지만 해당 프로그램의 참여가 필요치 않다고 판단된다면 어떡해야 할까? 원칙적으로는 그를 제외하는 것이 옳을 것이다. 
하지만 당사자가 경험할 거부와 상실감 때문에 프로그램 참여에서 제외하는 것이 쉽지 않다.
그리고 첫 번째의 문제 때문에 그를 쉽게 포기하지 못하기도 한다.

이때의 해결책은 다음과 같다.
대안 프로그램을 검토하는 것이다. 복지관의 프로그램이 다양하다면, 더 적절한 프로그램을 추천할 수 있을 것이며, 다른 기관의 프로그램을 추천할 수도 있을 것이다.
이는 해당 프로그램의 기획 단계에서 미리 검토되어야 한다.

지금까지 사업계획서 또는 프로그램 기획서를 작성함에 있어 이런 내용들은 잘 포함되지 않고 있다.
만일 당신이 경력이 좀 있는 사회복지사라면 이런 내용을 포함함으로써 자신의 기획역량을 한 단계 더 높일 수 있을 것이다. 
만일 당신이 슈퍼바이저라면 어느 정도 해당 사업에 숙달된 사회복지사에게 해당 내용을 슈퍼비전하고 점검할 수 있을 것이다. 이 때에는 반드시 위 내용들을 충분히 검토해 단계별로 전달하는 것이 중요하다.

STATA가 버전이 바뀌면서 table의 옵션이 바뀌었다.

기존의 버전에서는 table의 옵션에 contents가 있어서, 평균, 표준편차 등을 행으로 해서 비교가 가능했었다.

흔히들

.table 변수1 변수2, c(평균 표준편차)

위와 같은 형태로 사용했었다. 

하지만 이젠 이 옵션이 사라진 것이다.

STATA 17 버전에서 table의 sysntax를 살펴보면,

따라서 17버전에서는 해당 명령어를 달리해야만 내용을 확인할 수 있다.

예를 들어, 아래와 같이 바꿔줘야만 한다.

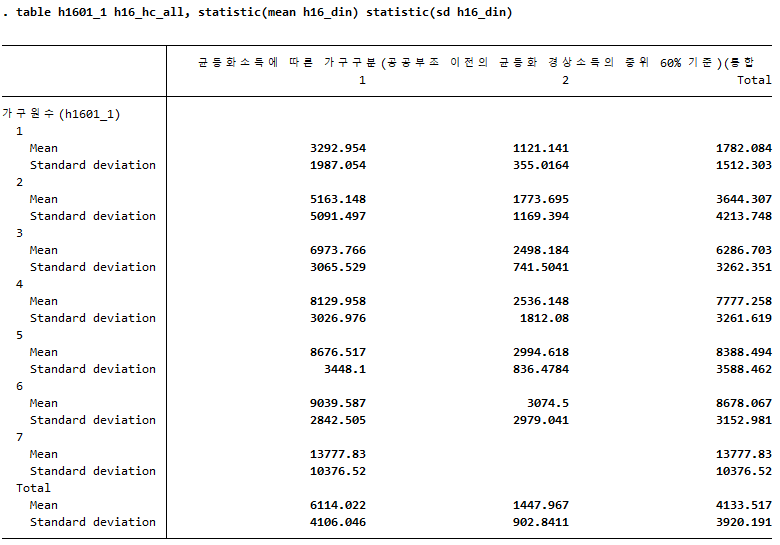
.table h1601_1 h16_hc_all, c(mean h16_din sd h16_din)
→ .table h1601_1 h16_hc_all, statistic(mean h16_din) statistic(sd h16_din)

만일, 2개 이상의 변수에서 평균을 보고자 한다면, 같은 방식으로 병기해주면 된다.
예) .table h1601_1 h16_hc_all, statistic(mean h16_din h16_cin) statistic(sd h16_din h16_cin)

구버전에서는 c() 안에 mean, sd, max 등을 같이 나타낼 수 있었으나, 새버전에서는 평균은 mean으로 묶고, 표준편차는 sd로 따로 묶어주어야만 제대로 된 값을 출력해준다.

보통 외부 패키지를 설치하고자 할때는 

.findit 패키지명

이렇게 검색하고, 거기서 바로 클릭해 설치를 합니다.

하지만 간혹 서버가 닫히면 패키지를 다운받을 수 없어 설치가 안됩니다.

오늘 wls0 패키지를 다운받으려고, 
.findit wls0
이렇게 했는데, 갑자기 안보이는 겁니다.
https://stats.oarc.ucla.edu/stat/stata/ado/analysis/
여기에서 제공하고 있었는데, 404 Forbidden이 뜨면서 연결이 안되었습니다.
https://stats.oarc.ucla.edu/stata/ado/analysis/

위와 같이 다운링크가 수정되었는데, 반영이 안되었나봅니다.

여기서 wls0를 클릭하셔서 직접 다운받으시면 됩니다.

그리고 다른 사람이 해당 패키지를 이미 갖고 있다면 그 파일을 복사해서 설치할 수도 있습니다.

일단, 해당패키지가 설치된 주소를 알아야 하는데,
C:\Users\사용자계정\ado\plus\
여기에 해당 알파벳 폴더에 패키지가 있습니다.
wls0는 C:\Users\사용자계정\ado\plus\w 폴더에 있습니다.

여기서 두 파일을 복사해야합니다.
****.ado
****.sthlp 또는 ****.hlp

만일 wls0라면 각각 wls0.ado, wls0.hlp가 될겁니다.

https://stats.oarc.ucla.edu/ 여기서 Softwares > Stata 찾아들어가시면,

Advanced Usage에 Stata Programs for Research and Teaching 링크가 있습니다.

바로 아래 링크가 그것입니다.

그리고 다시한번 IDRE Stata programs for data analysis 링크를 클릭하시면,

여기서 wls0를 클릭해 다운받으시면 되며, 그외 다른 다양한 패키지도 확인하실 수 있습니다.

https://stats.oarc.ucla.edu/stata/ado/analysis/

그리고 이 두 파일을 내 컴퓨터의 똑같은 경로에 붙여넣기만 하면 됩니다.
만일 해당 알파벳 폴더가 없다면 새로 만드시면 됩니다.
wls0는 w 폴더에 넣으시면 됩니다.

이제 STATA에서
.help wls0
이렇게 하시면 wls0의 용례(syntax)를 확인할 수 있으며, 분석도 가능해집니다.