검색결과 리스트
전체 글에 해당되는 글 804건
- 2024.06.21 컴퓨터 예약 종료 배치파일(.bat) 만들기
- 2024.06.17 소모품 구매 및 물품 계약구매(수의계약)에 따른 징구서류 검토
- 2024.06.02 다중응답에 대한 카이제곱(χ²) 검정 방법 by SPSS
- 2024.05.29 도시가스 사용시설의 안전관리자 선임기준
- 2024.05.29 yt-dlp를 쉽게... 배치파일(bat) 만들기 1
글
컴퓨터 예약 종료 배치파일(.bat) 만들기
컴퓨터를 켜놓은 채 나가야하는 경우, 예약 종료 기능을 사용하면 편리하겠다 생각해본 적 없는가?
cmd 창을 띄우고, shutdown 명령어를 사용하면 되지만, 이런 명령어 입력에 익숙치 않다면, 배치 파일(.bat)을 만들어 두면 유용하게 사용할 수 있다.
메모장을 열고 아래 초록색 박스 안의 내용을 복사해 붙여넣으면 된다.
이후 저장할 때 파일 형식을 "모든 파일(*.*)"을 선택한 후, 확장자를 bat로 해서 저장하면 된다.
| @echo off echo ============================================ echo 예약 종료 또는 예약 종료 취소를 실행합니다. echo ============================================ @set /p onoff="예약종료=1, 예약종료취소=2:" if %onoff%==1 goto on if %onoff%==2 goto off : on echo 예약 종료 시간을 설정합니다. echo ============================================ @set /p poweroff=몇 시간 뒤에 종료할까요? : set /a offhour=%poweroff%*3600 shutdown /s /t %offhour% goto end : off echo 예약 종료를 취소합니다. pause shutdown /a goto end : end echo. echo 설정이 완료되었습니다. echo ============================================ pause |
사실 필요한 명령어는
shutdown /s /t "종료까지 필요한 시간(초)"라는 명령어 한줄이다.
하지만 이 경우 초단위로 설정하게 된다.
익숙한 시간 단위로 변환할 수 있도록 명령어를 수정했고,
한번 설정하면 이걸 해제해야지만 새로 설정이 가능하다.
하여 예약종료를 취소하는 메뉴까지 추가해서 파일을 구성해보았다.
이때 주의할 점, 반드시 인코딩을 ANSI로 해야 한글이 깨지지 않는다.
모르겠으면 아래 첨부파일을 다운 받아서 그냥 실행해도 된다.
'[정보] IT정보&활용' 카테고리의 다른 글
| [구글 Apps Script] PDF로 출력하기 (0) | 2024.10.23 |
|---|---|
| [구글 스프레드 시트] 서명받기 (0) | 2024.08.27 |
| yt-dlp를 쉽게... 배치파일(bat) 만들기 (1) | 2024.05.29 |
| 한글, ( )안의 글자만 모양 바꾸기 (0) | 2023.03.30 |
| [엑셀] 파일명 구하기 (0) | 2022.10.18 |
설정
트랙백
댓글
글
소모품 구매 및 물품 계약구매(수의계약)에 따른 징구서류 검토
2024.06.25 - [[정보] 복지 이야기/[法] 복지관련 법령] - 사회복지시설에서의 구매거래에 따른 지출 방법 정리
수의계약에 대해서는 「지방자치단체를 당사자로 하는 계약에 관한 법률」과 이에 따른 「지방자치단체 입찰 및 계약집행기준」을 통해 확인할 수 있다.
이때 1천원짜리 볼펜 한 자루를 구입하는 것도 수의계약에 의한 구매를 하고, 필요한 서류를 모두 징구해야만 하는 것일까?
우선 확인해야하는 용어는 “물품”과 “소모품”이다.
「사회복지법인 및 사회복지시설 재무·회계규칙」 제38조 및 제40조의2에 따르면, 물품이란 자산가치가 있는 것으로 우리가 흔히 얘기하는 비품으로 관리가 필요한 것을 말한다. 한편 사무용품 등 업무에 사용하는 물건 등은 “소모품”이라고 말한다.
지방계약법에서 계약을 통해 구매해야하는 물품이라는 것은 바로 이 자산가치가 있는 비품에 해당하는 것이라 보아야 할 것이다.
이를 전제하고 일반적인 수의계약에 따르는 물품 구매 금액기준과 징구서류를 확인해보면 다음과 같다.
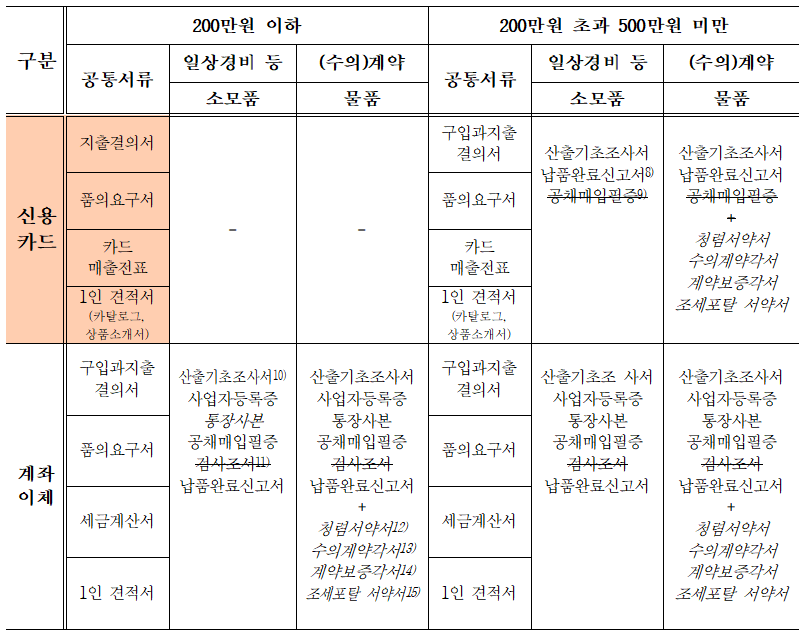
위 표에서 확인할 수 있듯이, 200만원 이하의 소모품 또는 물품(비품)을 신용카드로 구입시 필요한 서류는 지출결의서, 품의요구서, 카드매출전표, 1인 견적서(카탈로그, 상품소개서)로 끝난다. 하지만 현금으로 구입하려면 산출기초조사서를 비롯해 많은 서류가 더 필요하며, 물품이라면 수의계약에 따른 청렴서약서, 각서 등을 추가로 받아야만 한다.
보다 자세한 내용은 첨부파일을 확인하자.
※ update 2024. 6. 24.
관련 세부 근거 등을 각주로 추가하였습니다.
'[楞嚴] 생각 나누기 > [法] 복지 실무법제' 카테고리의 다른 글
| 기부금단체의 의무 3가지 (0) | 2022.09.14 |
|---|---|
| 사회복지시설 종사자 채용시 장애인학대범죄경력조회 추가 (0) | 2022.03.04 |
| 대법원 2021. 10. 15. [ 2021다227100 ] 판결에 대한 요약 및 쟁점 해석 (0) | 2021.10.20 |
| 사회복지시설 운영과 관련하여 검토 대상 법률들의 목록 (0) | 2021.08.27 |
| 민간위탁에 따른 사무편람 (0) | 2021.07.02 |
설정
트랙백
댓글
글
다중응답에 대한 카이제곱(χ²) 검정 방법 by SPSS
SPSS 다중반응 변수를 처리하다보면 두 가지 불편한 점을 만나게 된다.
하나는 다중반응에 대한 변수군을 정의한 것은 저장되지 않는다는 사실이다. 따라서 컴퓨터를 껐다가 새로 켜서 분석을 하려하면 그때마다 매번 변수군을 새로 정의해야만 한다.
다른 하나는 다중반응에 대해 교차분석을 하면 교차표만 제공해줄 뿐 카이제곱검정 등 검정통계량을 알려주지는 않는다.
이 두 가지는 생각보다 불편하다.
이와 관련하여 두번째는 다음과 같은 절차를 통해서 확인할 수 있다.

1. 다중반응 변수군을 정의한다.
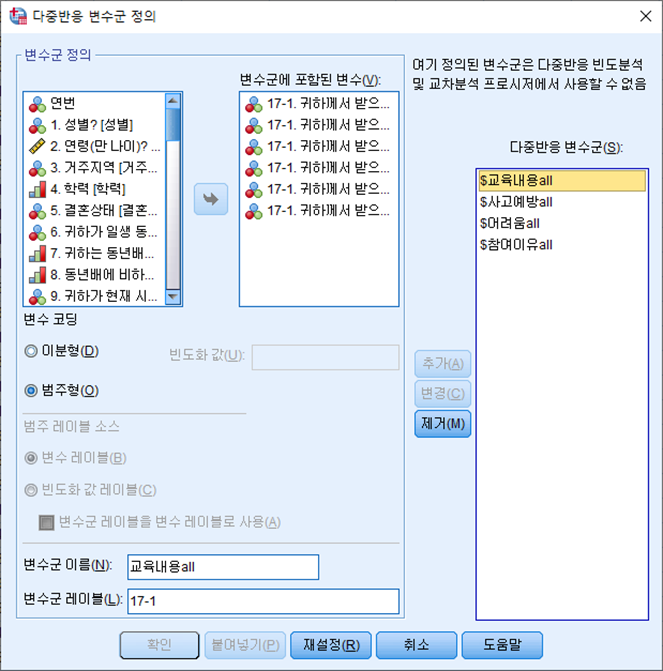
2. 사용자 정의 표를 통해 분석할 변수를 입력한다.
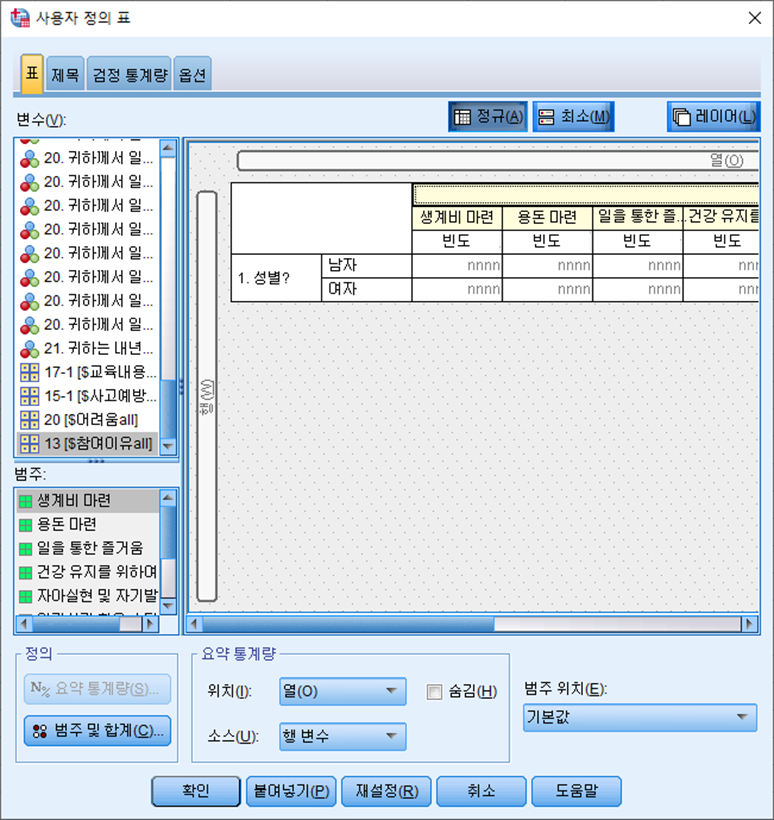
- 이때 독립변수를 행(W)에, 종속변수를 열(O)에 마우스를 이용해 끌어다 놓는다.
3. 검정통계량 탭에서 옵션을 선택한다.
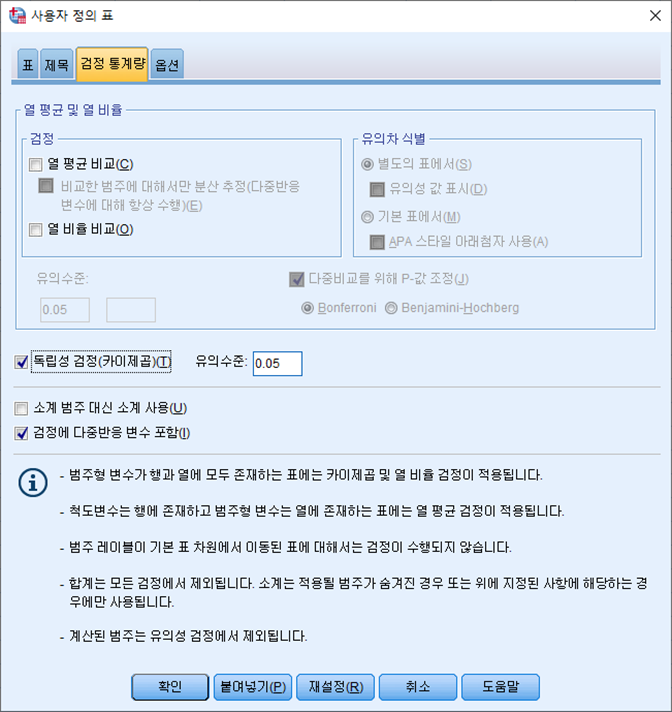
- 여기서 [□ 독립성 검정(카이제곱)(T)]을 체크해준다.
4. 결과를 확인한다.

- 위 결과에서 보듯이, 성별에 따른 노인일자라시압 참여이유에 대한 검정결과 χ²=125.399(p<.01)로 나타난 것을 확인할 수 있다.
'[楞嚴] 생각 나누기 > [平] 사회조사와 데이터분석' 카테고리의 다른 글
| 구글 스프레드 시트로 데이터 분석하기 (1) | 2024.07.28 |
|---|---|
| Excel로 통계분석하기 #3 (0) | 2024.05.27 |
| 알아두면 쓸모있는 통계관련 잡학상식 (0) | 2023.12.11 |
| 표본오차(sampling error) (2) | 2023.11.01 |
| 리커트(Likert) 척도는 서열척도인가? (0) | 2023.11.01 |
설정
트랙백
댓글
글
도시가스 사용시설의 안전관리자 선임기준
사회복지시설 중 많은 시설들이 도시가스를 사용하고 있다.
이 경우 안전관리자를 선임해야만 하는 것일까?
이에 대해서는 「도시가스사업법」을 살펴볼 필요가 있다.
결론만 개략적으로 얘기해보자면,
사회복지시설이면서, 도시가스 사용량이 월 1,000㎥ 이상이면 안전관리자를 선임하여야한다.
이때 도시가스 사용량은 도시가스를 사용하는 연소기의 소비량을 기준으로 계산하면 된다.
또한, 계량기로부터 연소기까지의 배관이 건물 벽이나 바닥에 매립된 경우, 별도로 시장이 지정한 경우 등은 안전관리자를 선임해야만 한다.
끝으로 액화천연가스(LNG)의 저장탱크가 있다면, 안전관리자를 선임해야한다.
자세한 내용은 첨부파일을 참조하자.
설정
트랙백
댓글
글
yt-dlp를 쉽게... 배치파일(bat) 만들기
컴퓨터로 업무를 보다보면, 단순 반복 등 간단한 업무는 자동화할 수 없을까 하는 생각을 하게 된다.
https://github.com/ 같은 곳에서 유용한 프로그램을 발견했을 때도 마찬가지이다.
예를 들면, yt-dlp 같은 것이다. https://github.com/yt-dlp
yt-dlp는 Windows용 실행파일을 제공한다.
https://github.com/yt-dlp/yt-dlp?tab=readme-ov-file#installation
하지만 단순한 더블클릭만으로는 실행되지 않는다.
즉 간단한 DOS 명령어를 알지 못한다면 그림의 떡인건 마찬가지이다.
이때 이를 위한 배치파일(bat)을 만들어두면 아주 유용하다.
우선 이 실행파일은 cmd 창에서 실행해야하며, 프로그램이 있는 위치(경로)로 이동해야하고, 다운로드할 링크 주소를 별도로 입력해주어야 한다.
yt-dlp
yt-dlp has 13 repositories available. Follow their code on GitHub.
github.com
| C:\Users\내계정>_ C:\Users\내계정>cd C:\yt-dlp C:\yt-dlp>yt-dlp.exe https://youtube.com/watch?v=a123456 |
게다가 구체적인 옵션을 부여하려면 더 복잡해진다.
생각을 단순화해보자.
1. Windows에서 더블클릭만으로 실행되었으면 좋겠다.
2. 실행하면, 친절하게 무엇을 입력할지 안내해주면 좋겠다.
자, 이제 yt-dlp.bat 파일을 만들어보자.
메모장을 열고 다음과 같이 입력한다.
| set /p url=Enter Youtube URL : yt-dlp %url% |
이제 끝났다.
이 파일을 yt-dlp.exe가 있는 폴더에 같이 저장하기만 하면 된다.
set /p url= // 입력하는 내용을 url이라는 변수에 저장
%url% // url에 입력된 값을 표현
yt-dlp %url% // yt-dlp 명령어(실행프로그램)에 더해 url이라는 변수에 저장된 내용을 자동으로 입력해준다.
-----------------------------------------------------------------------
세상에 나와 같은 생각을 하는 사람은 아주 많고, 이들은 더욱 전문적인 배치파일을 만들어 배포하고 있다.
https://github.com/edinsuta/yt-dlp-batch
GitHub - edinsuta/yt-dlp-batch: Simple batch files for simplifying basic usage of https://github.com/yt-dlp/yt-dlp (a fork of ht
Simple batch files for simplifying basic usage of https://github.com/yt-dlp/yt-dlp (a fork of https://github.com/rg3/youtube-dl) Windows .exe releases - edinsuta/yt-dlp-batch
github.com
같은 방식으로 업데이트도 만들 수 있다.
※ 참고로 배치파일의 내용은 한글도 입력이 가능하지만, 많은 경우 오류(특히 주석)가 생긴다.
그러니 최소한의 쉬운 영어로 입력할 것을 권고한다.
- (덧붙임) -------------------------------------
FFmpeg를 설치하면 더욱 좋습니다.
1. http://ffmepg.org 에서 파일을 다운받습니다.
https://ffmpeg.org/download.html#build-windows
※ 아래 두 종류 중 아무거나 받으시면 됩니다.
- https://www.gyan.dev/ffmpeg/builds/
- https://github.com/BtbN/FFmpeg-Builds/releases
2. 압축파일을 풀어서 아래 경로에 복사합니다.
C:\Program Files\FFmpeg
3. 경로(path)를 추가합니다.
- cmd 창에서 아래를 복사&붙여넣기 하셔서 실행하시면 됩니다.
set path="%PATH%";C:\Program Files\FFmpeg\bin
- (덧붙임2) -------------------------------------
현재 경로를 확인하거나 변수로 지정하는 방법
%cd%
예)
set /p current_path=%cd%
# 현재경로를 current_path라는 변수에 저장
xcopy "%cd%" "D:\" /e
# 현재 경로의 모든 파일과 (하위)폴더를 D:\로 복사
'[정보] IT정보&활용' 카테고리의 다른 글
| [구글 스프레드 시트] 서명받기 (0) | 2024.08.27 |
|---|---|
| 컴퓨터 예약 종료 배치파일(.bat) 만들기 (0) | 2024.06.21 |
| 한글, ( )안의 글자만 모양 바꾸기 (0) | 2023.03.30 |
| [엑셀] 파일명 구하기 (0) | 2022.10.18 |
| 사용자 프로필 경로 확인하기 (0) | 2022.10.18 |

RECENT COMMENT