검색결과 리스트
가설검정에 해당되는 글 3건
- 2023.10.29 5. 가설의 검정과 유의확률
- 2023.10.29 4. 가설의 검정의 전제조건
- 2023.10.29 3. 가설 검정은 ‘무엇’으로 하는가?
글
5. 가설의 검정과 유의확률
앞선 예에서 우리는 “성별(A)에 따른 TV 시청 시간(B)에 평균의 차이가 없다.”는 영가설을 세웠다. 그리고 이 영가설을 검정하기 위해 통계기법을 활용해 데이터를 분석할 것이다. 그러면 그 결과로 ‘통계량’과 ‘유의확률(p)’을 얻게 될 텐데, 우리가 할 일은 이 유의확률로부터 영가설을 기각할 수 있을지 없을지를 결론내리는 일이다.
유의확률은 p 값(p value)라고도 하며, 0∼1 사이의 숫자로 p=.137과 같이 소숫점 셋째 자리까지 표시한다.
p<.05는 ‘유의확률이 0.05보다 작다’로 읽는다. 풀어 설명해보자면, 성별에 따른 TV 시청시간에는 평균의 차이가 없다(영가설)가 사실이라고 가정할 때, 해당 결과가 나타날 확률이 5%보다 작다는 뜻이다. 바꿔 얘기하면, 차이가 있다는 결과를 얻을 확률이 95%보다 크다가 된다.

따라서 영가설은 기각되고, 대립가설이 채택(지지)된다. 즉, TV 시청 시간과 시력 간의 평균 비교에 있어 유의미한 차이가 있다고 결론내리게 된다.
한편, p>.05라면 어떻게 될까? 이때에는 ‘영가설을 기각할 근거가 충분하지 않다’고 말한다. 이때 이것이 영가설을 채택한다고 말하는 것은 아니다. 또한 통계적으로 유의미하지 않았다(nonsignificant)는 것이 무의미하다(insignificant)는 뜻은 아니다. 따라서 표현에 주의해야한다.
'[楞嚴] 생각 나누기 > [平] 사회조사와 데이터분석' 카테고리의 다른 글
| 7. 제1종 오류는 왜 일어나는가? 해결방법은? (0) | 2023.10.29 |
|---|---|
| 6. 영가설 기각의 의미 (0) | 2023.10.29 |
| 4. 가설의 검정의 전제조건 (0) | 2023.10.29 |
| 3. 가설 검정은 ‘무엇’으로 하는가? (0) | 2023.10.29 |
| 2. 영가설을 표현하는 두 가지 방법 (0) | 2023.10.29 |
설정
트랙백
댓글
글
4. 가설의 검정의 전제조건
이제 가설을 검정해 볼 차례이다. 이때 한 가지 짚고 갈 것이 있다.
우리가 조사 대상 ‘전체’에 대해 설문 등을 실시하여 결과값들을 얻었다면, 그 결과는 그 자체로 사실이 된다. 예를 들어 인구주택총조사가 그렇다. 매 5년마다 대한민국 국민 전체를 대상으로 조사를 실시한다. 따라서 그 조사 결과는 그대로 사실이다.
하지만 많은 경우 전수를 조사하는 것은 비용과 시간이 많이 든다. 하여 우리는 대부분 표본(sample)을 뽑아서 그 결과를 분석한다. 이때는 당연히 이 표본이 전체 조사 대상(모집단)을 대표할 수 있다는 확신이 있어야 한다. 즉 표본조사의 결과값(모수 추정)이 전수조사의 결과값(모수)과 차이가 거의 없을 것을 전제한다.


여기서 등장하는 용어들은 모집단을 대상으로 하는가, 표본집단을 대상으로 하는가에 따라 약어 기호 표시들이 조금씩 다르다. 만일 앞선 전제를 충족하였다면 굳이 이 둘을 구분할 필요는 없다.
다시 돌아와 전제조건인 표본의 대표성 문제는 제대로 된 표본추출을 통해 해결이 된다. 연구자들은 표본이 모수를 정확히 추정할 수 있도록 하기 위해 표본을 뽑는(추출) 방법들에 대해 고민해왔고, 이런 표본추출방법은 확률표본추출과 비확률표본추출이 있다. 이 둘의 차이점은 딱 하나이다. 모집단의 구성원이 표본으로 선택될 확률이 동등하면 확률표본추출이라하고, 그렇지 않은 경우를 비확률표본추출이라 한다.

'[楞嚴] 생각 나누기 > [平] 사회조사와 데이터분석' 카테고리의 다른 글
| 6. 영가설 기각의 의미 (0) | 2023.10.29 |
|---|---|
| 5. 가설의 검정과 유의확률 (0) | 2023.10.29 |
| 3. 가설 검정은 ‘무엇’으로 하는가? (0) | 2023.10.29 |
| 2. 영가설을 표현하는 두 가지 방법 (0) | 2023.10.29 |
| 1. 영가설(零假設, null hypothesis, 귀무가설)이란? (0) | 2023.10.29 |
설정
트랙백
댓글
글
3. 가설 검정은 ‘무엇’으로 하는가?
가설검정은 결국 비교를 통해 이루어진다. 그렇다면 무엇을 비교하게 되는 것일까? 가장 단순하게 대답해보자면 “평균”이라고 말할 수 있다. 뒤에서 다룰 검정방법들도 결국은 평균과 편차를 기반으로 만들어진 수식들이다.
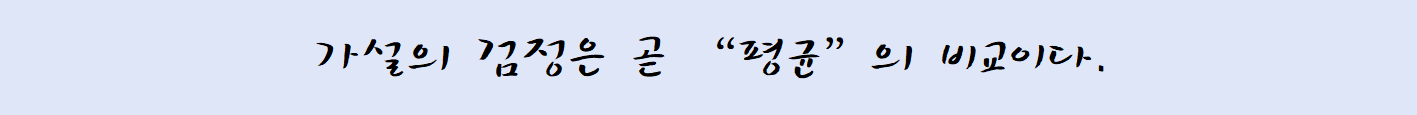
물론 이것이 전부인 것은 아니다. 평균을 구할 수 없는 경우도 많기 때문이다. 하지만 생각해보라. 여러분이 얘기하는 통계는 무엇으로 표현되는가? 단적으로 숫자라고 말할 수 있다. 숫자로 계산할 수 있는 것은 평균을 구할 수 있다. 즉 통계를 하겠다는 얘기는 곧 평균을 구하겠다는 말과 다르지 않다. 이를 ‘모수통계’라 한다.
만일 우리가 정한 변수가 성별, 결혼 여부 등과 같이 숫자로 계산할 수 없는 것들이라면 ‘비모수통계’의 방법을 사용해야만 할 것이다.
'[楞嚴] 생각 나누기 > [平] 사회조사와 데이터분석' 카테고리의 다른 글
| 5. 가설의 검정과 유의확률 (0) | 2023.10.29 |
|---|---|
| 4. 가설의 검정의 전제조건 (0) | 2023.10.29 |
| 2. 영가설을 표현하는 두 가지 방법 (0) | 2023.10.29 |
| 1. 영가설(零假設, null hypothesis, 귀무가설)이란? (0) | 2023.10.29 |
| Ⅲ. 가설은 어떻게 검정되는가? (1) | 2023.10.29 |

RECENT COMMENT